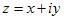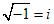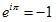La conjetura de Goldbach

Se trata de un problema abierto de la teoría de números más antiguo en matemáticas. El autor que lo formuló fue Christian Goldbach, matemático prusiano de Königsberg en 1690. La formulación de la llamada conjetura de Goldbach se gestó en la correspondencia entre el propio Goldbach y su amigo, Leonhard Euler.

A veces se lo califica del problema más difícil en la historia de esta ciencia. Concretamente, G.H. Hardy en 1921 en su famoso discurso pronunciado en la Sociedad Matemática de Copenhage comentó que probablemente la conjetura de Goldbach no es sólo uno de los problemas no resueltos más difíciles de la teoría de números, sino de todas las matemáticas.

Su enunciado es el siguiente:

Todo número par mayor que 2 puede escribirse como suma de dos números primos.

Christian Goldbach (1742)

Fórmula de Euler para poliedros

Nos adentramos en una de las fórmulas matemáticas más bellas, la fórmula de Euler para poliedros. Espacio dedicado a cuestiones geométricas de objetos que son más o menos cotidianos, lo poliedros, como por ejemplo el cubo, la pirámide triangular o tetraedro, el dodecaedro (cuyas caras son pentágonos), el icosaedro truncado (que es la pelota de fútbol), etc. Aunque los nombres nos suenen a chino, sin embargo, son objetos que vemos en nuestro día a día.

El estudio de los poliedros es de de vital importancia no solamente para el estudio geométrico de los mismos, para la investigación matemática, sino también para sus aplicaciones en campos tan diversos como por ejemplo química, mineralogía, biología, ingeniería, arquitectura, diseño (industrial o de objetos cotidianos) o incluso en el arte.

Matemáticos en primera persona

Diez matemáticos argentinos cuentan sobre su pasión por esta ciencia. Cómo descubrieron su vocación, cuáles son sus desafíos cotidianos y qué cosas los asombran de las matemáticas. Un material indispensable para saber quiénes son y qué hacen los matemáticos de nuestro país.

Las Matemáticas son para siempre

Excelente!! Buen discurso, entretenido, divertido acerca de las matemáticas!
Para disfrutarlo!

Eduardo Sáenz de Cabezón

Licenciado en Teología y Doctor en Matemáticas, es autor de varias charlas divulgativas sobre su área que imparte en universidades y centros de educación secundaria. Es narrador oral para niños, jóvenes y adultos.
Nació en Logroño, España, en 1972. Recibido en la Universidad Pontificia de Comillas, en 1996, además obtuvo su Licenciatura y Doctorado en Matemáticas en la Universidad de La Rioja.
Ejerce como Profesor de las asignaturas Informática, Sistemas Informáticos, Matemática Discreta y Álgebra, en la Universidad de La Rioja, desde 2010. También es tutor de Trabajos de Grado y Maestría en las titulaciones de Informática y Matemáticas.
Publicó artículos de investigación y es autor del show matemático “El baúl de Pitágoras”, que fue exhibido en teatros y bares en varias ciudades de España desde 2012. Ganó el concurso de monólogos científicos FameLab en España, 2013. Es uno de los fundadores del grupo de monologuistas científicos “The Big Van Theory” con más de 200 representaciones en España entre 2013 y 2014.

Más información disponible en TEDxRíodelaPlata

Gráfico III

También puedes ver la entrada Gráfico I y Gráfico II

Jugamos con la geometría?

Uno de los requisitos necesarios para que una actividad sea considerada como juego es el hecho de estar sometida a unas reglas. Al igual que existen unas reglas en el juego de la ajedrez, las matemáticas también se rigen por unas "reglas universales" y su descubrimiento suponen todo un reto a los estudiantes.

Gracias a herramientas como Geogebra, resulta tremendamente sencillo organizar competiciones en las cuales, los diferentes equipos en los que se puede dividir la clase, podrán experimentar con la Geometría Dinámica, establecer sus propias hipótesis y acabar desvelando las reglas que ésta encierran.

Debemos tener presente que para que el juego tenga una eficiencia pedagógica, éste ha de ser auto-educativo[1]. El docente debe permanecer lo más retirado posible de las dialécticas que se establezcan entre los jóvenes, minimizando sus participación a la organización de los grupos y facilitar los aspectos logísticos en los que se desarrollará la actividad. La Teoría de Situaciones de Guy Brosseau se brinda especialmente a este tipo de ejercicios:

"La devolución es el acto por el cual el enseñante hace aceptar al alumno la responsabilidad de una situación de aprendizaje (adidáctica) o de un problema, y acepta él mismo las consecuencias de esta transferencia.”
---------------
[1] C. Krou, “La fonction éducative du jeu”, Dossiers pédagogiques, op. cit., p. 9.

Visto en MiPizarraDeMates

Matemática

En esta oportunidad hablaremos de la estrecha relación entre las matemáticas y el arte. Empezamos con una prueba de "agudeza visual": ¿cuántas "rectas" se pueden formar a partir de los 7 puntos (A, B, C, D, E, F,G) que hay en el plano proyectivo de la figura?

Definiciones:

Plano proyectivo: Un plano proyectivo verifica los tres axiomas de incidencia AIi, el postulado elíptico de las rectas paralelas y la propiedad de que en cada recta hay al menos 3 puntos.

Axiomas de incidencia:

• Ax. I 1: Dados 2 puntos diferentes del plano, existe una única recta que pasa por ellos.
• Ax. I 2: En cada recta hay al menos 2 puntos.
• Ax. I 3: Existen 3 puntos tales que no hay ninguna recta que pase por los 3 puntos a la vez.

Postulado elíptico: Para toda recta "l" y todo punto "P" que no está en ella, no existe ninguna recta "m" que pase por "P" y que sea paralela a "l".

Visto en MiPizarraDeMates 

Gráfico II

El tablero de ajedrez es invertido por una función compleja como f(z) = 1/z, donde "z" es "x + iy".

Los cuadrados son curvos pero aún forman ángulos rectos entre sí.

También puedes ver la entrada Gráfico I

Nube de tags

Una nube de palabras o nube de etiquetas es una representación visual de las palabras que conforman un texto, en donde el tamaño es mayor para las palabras que aparecen con más frecuencia.

Las etiquetas son palabras clave que suelen estar ordenadas alfabéticamente o, en ocasiones, agrupadas semánticamente. La importancia de una etiqueta se muestra con el tamaño de la fuente y/o color.

Ejemplo de una Nube de Tags

La historia de las Matemáticas

Historia de la Matemática en un comic

Diccionario Ilustrado de Conceptos Matemáticos - Efraín Soto Apolinar

Bibliografía:

• Soto Apolinar, E. (2011) Diccionario ilustrado de conceptos matemáticos. (3er ed.). México.

Diccionario ilustrado de conceptos matemáticos - Soto Apolinar Efraín from Federico Gabriel Gutierrez

Los poliedros convexos

Diez herramientas TIC para innovar en el aula

Comparto un interesante artículo sobre “Diez herramientas TIC para innovar en el aula”

Acceda al artículo desde: AQUÍ

Visto en: ineverycrea.net | Imagen: Google Images

Pi, la identidad de Euler y los dados matemáticos

Dados…seguro que has visto dados de todo tipo. Desde los habituales con seis caras y los números 1, 2, 3, 4, 5 y 6 hasta dados con menos caras o con otros números u otro tipo de inscripciones en ellas.

Y, cómo no, las matemáticas tienen mucho que decir a la hora de innovar en el mundo de los dados. El último ejemplo sobre esto del que he tenido constancia es el que nos presentaba Javier Omar en La Covacha Matemática hace unos días. Magníficas creaciones de Matt Chisholm en forma de dado cúbico cuyas caras llevan inscritos los siguientes números:

con los que, por ejemplo, podemos formar la identidad de Euler

o recrear una propiedad de

Identidad de Euler

Leonard Euler fue un gran matemático y físico, nacido en 1707 en Basilea (Suiza). Es considerado el mejor matemático de siglo XVIII y uno de los mejores de la historia. 

Aportó grandes ideas en los campos del cálculo, geometría, lógica, teoría de números, hidrodinámica, mecánica, electromagnetismo y demás. Fue verdaderamente un genio.

Cuando estaba trabajando en el cálculo complejo, Euler dedujo la que tal vez sea la ecuación más elegante y magnífica de todas.
Un número complejo es aquél que se representa mediante una parte real y una parte imaginaria, si definimos a "z" como un complejo, "x" su parte real e "y" su parte imaginaria, este quedaría así,

Donde "i" es el número imaginario, definido como la raíz cuadrada de -1,

Ahora, si tomo al famoso numero "e" y lo potencio con el número complejo "z",

Mediante series numéricas, Euler encontró que,

Por lo tanto,

Esta es conocida como la fórmula de Euler, que define la exponenciación compleja. Es una fórmula de gran sutileza y precisión. Pero si hacemos un análisis más minucioso podemos llegar a más aún.
Si hacemos que "x" valga 0 y que "y" tome el valor de pi,

A su vez, sabemos que el seno de pi es cero y el coseno de pi vale -1, entonces,

 

 

Ó, resulta lo mismo escribir,

Esta es la identidad de Euler, la ecuación más famosa de la matemática. En ella se puede decir que está resumida toda la matemática. Encontramos los conceptos de suma, multiplicación, exponenciación e identidad. Tenemos también, los cinco números fundamentales, el cero, el uno, pi, el número e y el número i.
Esta ecuación expresa con unos pocos símbolos matemáticos, una belleza infinita. Digna de un genio como Euler.

Infografía Interactiva

En esta oportunidad comparto con ustedes una infografía interactiva (para visualizarla debes tener java instalado).

Producción Multimedia (videos y animaciones)

Producción multimedia (videos y anomaciones) - Conectar Igualdad from Federico Gabriel Gutierrez

El número e=2,71...

Si se introduce el número e, uno de los números reales más importantes, a la manera matemáticamente formal, quizás dé un poco de miedo. Así que lo haré de una forma, si no divertida, al menos curiosa. Para ello prácticamente transcribiré parte de un libro cuyo título es "Matemática, ¿estás ahí?". Su autor es Adrián Paenza (doctor en Matemática, profesor y también un reconocido periodista en los ámbitos deportivo y político).

Empecemos.


Supongamos que una persona tiene un capital de 1 euro. Y vamos a suponer también que el interés que le pagan anualmente por ese euro es del 100%. Es sólo un ejemplo, ya sabemos que no existe ni existirá tal banco, pues se arruinaría antes de empezar. Pero da igual, será un ejemplo que nos servirá. Así que seguid el razonamiento.

Capital: 1 euro

Interés: 100% anual

Si uno hace la inversión en el banco y se va a su casa, ¿cuánto dinero tiene cuando vuelve justo al año? Está claro, como el interés es del 100%, al año el señor tiene 2 euros: uno que corresponde a su capital y otro que es producto del interés que le pagó el banco.

Capital al cabo de un año: 2 euros

Supongamos ahora que el señor decide poner su dinero no a un año, sino sólo a seis meses. El interés (a lo largo de todo este ejemplo) permanecerá constante: siempre será de un 100%. Al cabo de seis meses entonces, el señor ¿cuánto dinero tiene? Está claro que tiene 1,5 euros.

Esto es porque como invirtió el mismo capital de 1 euro a un interés del 100% pero sólo durante la mitad del año, le corresponde un interés de la mitad de lo que invirtió y, por eso, le corresponden 0,5 euros de interés. Es decir, su nuevo capital es de 1,5 euros.

Si ahora el señor decide reinvertir su nuevo capital en el mismo banco, con el mismo interés (100%) y por otros seis meses para llegar nuevamente al año como antes, ¿cuánto dinero tiene ahora?

Nuevo capital: 1,5 euros

Interés: 100% anual

Plazo que lo deposita: 6 meses

Al finalizar el año tiene:

¿Por qué? Porque el capital que tenía a los seis meses iniciales no se toca: 1,5 euros. El nuevo interés que cobra es de la mitad del capital, porque el dinero lo pone a un interés del 100% pero sólo por seis meses. Por eso, tiene 1/2·(1,5) = 0,75 como nuevo dinero que le aporta el banco como producto de los intereses devengados.

MORALEJA: al señor le conviene (siempre que el banco se lo permita) depositar el dinero en primer lugar a seis meses y luego renovar el plazo fijo a otros seis meses. Si comparamos con lo que le hubiera correspondido en el primer caso, al finalizar el año tenía 2 euros. En cambio, reinvirtiendo en la mitad, al cabo de 365 días tiene 2,25 euros.

Supongamos ahora que el señor coloca el mismo euro que tenía originalmente, pero ahora por cuatro meses. Al cabo de esos cuatro meses, reinvierte el dinero, pero por otros cuatro meses. Y finalmente, hace una última reinversión (siempre con el mismo capital) hasta concluir el año. ¿Cuánto dinero tiene ahora? Veamos.

Al principio del año el señor tiene:

A los cuatro meses (o sea, transcurrido 1/3 del año) tiene:

A los siguientes cuatro meses (ocho desde el comienzo) tiene:

Esto sucede porque a los cuatro meses el capital es de (1+1/3) y, al cabo de otros cuatro meses, tendrá el capital más un tercio de ese capital. La cuenta que sigue despues se obtiene de sacar factor comun (1+1/3) en el primer miembro de la igualdad.

Ahora bien: cuando el señor invierte (1+1/3)2 por otros cuatro meses, al llegar justo el fin del año, el señor tendrá el capital (1+1/3)2 más 1/3 de ese capital. O sea:

Como hemos visto de que ahora nos queda hacerlo no sólo cada cuatro meses, sino cada tres meses. Al cabo de un año el señor tendrá:

Si lo hiciera cada dos meses, tendría que reinvertir su dinero seis veces al año:

Si lo hicera una vez al mes, reinvirtiría doce veces por año:

Al señor le conviene poner su dinero a plazo fijo, pero haciéndolo con un plazo cada vez más corto y reinvirtiendo lo que obtiene (siempre con el mismo interés).

Supongamos que el banco le permitiera al señor renovar su plazo diariamente. En este caso, el señor tendría:

Y si lo hiciera una vez por hora, como en el año hay 8.760 horas, tendría:

Y si se le permitiera hacerlo una vez por minuto, como en el año hay 525.600 minutos, su capital resultaría ser:

Y, por último, supongamos que le permitieran hacerlo una vez por segundo. En este caso, como en el año hay 31.536.000 segundos el capital que tendría al cabo de un año sería:

MORALEJA: si bien uno advierte que el dinero al finalizar el año es cada vez mayor, el dinero que uno tiene al final no aumenta indiscriminadamente.

Hagamos un resumen de la lista que acabamos de escribir, en la que aparezca las veces al año que renueva su capital y su capital final:

1 vez al año - 2

2 veces al año - 2,25

3 veces al año (cuatrimestral) - 2,37037037...

4 veces al año (trimestral) - 2,44140625...

6 veces al año (bimestral) - 2,521626372...

12 veces al año (mensual) - 2,61303529...

365 veces al año (diario) - 2,714567475...

8.760 veces al año (por hora) - 2,718126664...

525.600 veces al año (una vez por minuto) - 2,718279243...

31.536.000 veces al año (una vez por segundo) - 2,718281785...Lo que es muy interesante es que estos números, si bien crecen cada vez que el interés se cobra más frecuentemente, no lo hacen en forma ni arbitraria ni desbocada. Al contrario: tienen un tope, están acotados. Y la cota superior (es decir, si uno pudiera imaginariamente estar renovándolo a cada instante) es lo que se conoce como el número e (que es la base de los logaritmos naturales o neperianos). No sólo es una cota superior, sino que es el número al cual se está acercando cada vez más la sucesión que estamos generando al modificar los plazos de inversión.El número e es un número irracional, cuyas primeras cifras decimales son:

El número e es uno de los números más importantes de la vida cotidiana, aunque su relevancia está generalmente escondida para el gran público. Habría que divulgar mucho más sobre él. Por ahora, nos contentamos con celebrar su curiosa aparición en este escenario, mostrándolo como el límite (y también la cota superior) del crecimiento de un capital de 1 euro a un interés del 100% anual y renovado periódicamente.

Visto en LasMatemáticas

Los números inversos de Fibonacci

Divide 1 entre 999.999.999.999.999.999.999.998.999.999.999.999.999.999.999.999, y mira lo que se obtiene:

¿Te has fijado en que los dígitos no nulos de la expresión decimal de este cociente son términos (en orden) de la sucesión de Fibonacci?

En la anterior tabla, los decimales están ordenados en bloques de 24 dígitos. Los últimos dígitos que aparecen en cada una de estos bloques son los términos de la serie de Fibonacci hasta el 116:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269, 2178309, 3524578, 5702887, 9227465, 14930352, 24157817, 39088169, 63245986, 102334155, 165580141, 267914296, 43349443, 701408733, 1134903170, 1836311903, 2971215073, 4807526976, 7778742049, 12586269025, 20365011074, 32951280099, 53316291173, 86267571272, 139583862445, 225851433717, 365435296162, 591286729879, 956722026041, 1548008755920, 2504730781961, 4052739537881, 6557470319842, 10610209857723, 7167680177565, 27777890035288, 44945570212853, 72723460248141, 117669030460994, 190392490709135, 308061521170129, 498454011879264, 806515533049393, 1304969544928657, 2111485077978050, 3416454622906707, 5527939700884757, 8944394323791464, 14472334024676221, 23416728348467685, 37889062373143906, 61305790721611591, 99194853094755497, 160500643816367088, 259695496911122585, 420196140727489673, 679891637638612258, 1100087778366101931, 1779979416004714189, 2880067194370816120, 4660046610375530309, 7540113804746346429, 12200160415121876738, 19740274219868223167, 1940434634990099905, 51680708854858323072, 83621143489848422977, 135301852344706746049, 218922995834555169026, 354224848179261915075, 573147844013817084101, 927372692193078999176, 1500520536206896083277, 2427893228399975082453, 3928413764606871165730, 6356306993006846248183, 10284720757613717413913, 16641027750620563662096, 26925748508234281076009, 43566776258854844738105, 70492524767089125814114, 114059301025943970552219, 184551825793033096366333, 298611126818977066918552, 483162952612010163284885.

Fíjate en las siguientes divisiones:

• 1/89 = 0,011235…, es decir, en la expresión decimal (y en bloques de 1 número) aparecen los 6 primeros números de la sucesión de Fibonacci;
• 1/9.899 = 0,0001010203050813213455…, es decir, en la expresión decimal (y en bloques de 2 números) aparecen los 11 primeros números de la sucesión de Fibonacci;
• 1/998.999 = 0,000001001002003005008013021034055089144233377610…, es decir, en la expresión decimal aparecen los 16 primeros números de la sucesión de Fibonacci.

Los números 89, 9.899, 998.999, etc. (y por supuesto, el número 999.999.999.999.999.999.999.998.999.999.999.999.999.999.999.999), se llaman números inversos de Fibonacci.

Los términos de la sucesión de Fibonacci se definen usualmente como: f₀=0, f₁=1, y f_n+2=f_n+1+f_n (si n≥0). Pero también pueden definirse a través de la función generadora G(x)=x/(1-x-x²), que cuando se expande en potencias dex, posee como coeficientes los términos de la sucesión de Fibonacci:

Observa finalmente que:

• G(1/10)=10/89,
• G(1/100)=100/9899,
• G(1/1000)=1000/998999,
• y en general, G(1/10ⁿ)=10ⁿ/(10²ⁿ-10ⁿ-1).

Es decir, los números inversos de Fibonacci son justamente los de la forma

10²ⁿ–10ⁿ–1.

El divisor de la división propuesta al principio

999.999.999.999.999.999.999.998.999.999.999.999.999.999.999.999 corresponde a n=16.

Visto en ZTFNews.org

Adictos a las redes sociales

Fuente: http://www.carlosnuel.com/wp-content/uploads/2013/05/infografia-adictos-a-las-redes1.jpg

Planeta web 2.0

Planeta web 2.0 from Federico Gabriel Gutierrez

Bibliografía

• Cobo Romaní, Cristóbal;Pardo Kuklinski,Hugo. 2007.Planeta Web 2.0. Inteligencia colectivao medios fast food. Grup de Recerca d'Interaccions Digitals,Universitat de Vic.Flacso México. Barcelona / México DF.

Problema de Haberdasher

Se trata de cortar un triángulo equilátero en cuatro piezas que formen también un cuadrado.
Fue propuesto por Henry Dudeney en 1902, y aquí está su solución, con las piezas unidas por el vértice que, a modo de bisagras, pueden girar para pasar de una figura a la otra.

Fuente: https://plus.google.com/u/0/+AdaGilIb%C3%A1%C3%B1ez/posts/CAKStmmebZH

Banda de Möbius

Es una superficie con una sola cara y un solo borde. Tiene la propiedad matemática de ser un objeto no orientable. También es una superficie reglada. Fue descubierta en forma independiente por los matemáticos alemanes August Ferdinand Möbius y Johann Benedict Listing en 1858.

La banda de Möbius posee las siguientes propiedades:

• Es una superficie que sólo posee una cara:

Si se colorea la superficie de una cinta de Möbius, comenzando por la «aparentemente» cara exterior, al final queda coloreada toda la cinta, por tanto, sólo tiene una cara y no tiene sentido hablar de cara interior y cara exterior.

• Tiene sólo un borde:

Se puede comprobar siguiendo el borde con un dedo, apreciando que se alcanza el punto de partida tras haber recorrido la totalidad del borde.

• Es una superficie no orientable:

Si se parte con una pareja de ejes perpendiculares orientados, al desplazarse paralelamente a lo largo de la cinta, se llegará al punto de partida con la orientación invertida. Una persona que se deslizara «tumbada» sobre una banda de Möbius, mirando hacia la derecha, al recorrer una vuelta completa aparecerá mirando hacia la izquierda.

• Otras propiedades:

Si se corta una cinta de Möbius a lo largo, se obtienen dos resultados diferentes, según dónde se efectúe el corte.

Si el corte se realiza en la mitad exacta del ancho de la cinta, se obtiene una banda más larga pero con dos vueltas; y si a esta banda se la vuelve a cortar a lo largo por el centro de su ancho, se obtienen otras dos bandas entrelazadas. A medida que se van cortando a lo largo de cada una, se siguen obteniendo más bandas entrelazadas.

Si el corte no se realiza en la mitad exacta del ancho de la cinta, sino a cualquier otra distancia fija del borde, se obtienen dos cintas entrelazadas diferentes: una de idéntica longitud a la original y otra con el doble de longitud.

Esta forma geométrica se utiliza frecuentemente como ejemplo en topología.

La Educación como práctica de la Libertad - Paulo Freire

En el Libro, Freire plantea la educación de las masas como el desafío fundamental de los países en desarrollo, una educación que, liberada de todos los rasgos alienantes, constituya una fuerza posibilitadora del cambio y sea impulso de libertad. Sólo en la educación puede nacer la verdadera sociedad humana y ningún hombre vive al margen de ella. Por consiguiente, la opción se da entre una pedagogía "para la domesticación" y una pedagogía "para la libertad", entre "educación para el hombre-objeto" y "una educación para el hombre-sujeto".

El autor considera que dentro de las condiciones históricas de la sociedad es indispensable una amplia concienciación de las masas a través de una educación que les permita reflexionar sobre su tiempo y su espacio. Está hondamente convencido de que la elevación del pensamiento del individuo, "que suele llamarse, apresuradamente, politización", comienza exactamente con esta autorreflexión que lo lleva a profundizar de su toma de conciencia y, sobre todo, a transformar su inserción en la historia, no ya como espectadores, sino como actor y autor.

Educación como práctica de la libertad - Paulo Freire from Federico Gabriel Gutierrez

Libros Digitales (Parte II)

Libros sobre Educación y TIC, investigaciones sobre el proceso de inclusión de TIC en la educación formal. Materiales didácticos, y acceso a aportes de calidad en el ámbito de la educación con tecnología.

Libros Digitales (Parte I)

Diez consejos para convertirte en un profesor inolvidable

Una infografía con diez consejos para convertirte en un profesor inolvidable.

www.aulaplaneta.com

Reflexión

Un trabajo cooperativo bien planteado, presenta incuestionables ventajas tanto para el aprendizaje como para la enseñanza. Si a ello le unimos que el trabajo sea original y creativo, podemos tener los elementos perfectos para atraer la atención del estudiante y mantener su motivación. En este sentido, la asignatura de matemáticas y la programación ofrecen enormes posibilidades para plantear situaciones didácticas de manera que los alumnos validen sus propios conocimientos teóricos, o bien desde un enfoque más constructivista (Piaget) plantear situaciones adidácticas de manera que los alumnos descubran por sí mismos, los conocimientos que les permitirán resolver el problema. Cuando seguimos esta metodología de trabajo, no se debe olvidar la fase final de "institucionalización" del saber por parte del profesor: 

"Por supuesto, todo puede reducirse a la institucionalización. Las situaciones de enseñanza tradicionales son situaciones de institucionalización pero sin que el profesor se ocupe de la creación del sentido: se dice lo que se desea que el alumno sepa, se le explica y se verifica que lo haya aprendido. Al principio los investigadores estaban un poco obnubilados por las situaciones adidácticas porque era lo que más le faltaba a la enseñanza tradicional.” Guy Brousseau (1994) 

Realidad Aumentada: la educación del futuro ya está presente

La Realidad Aumentada (RA) combina elementos virtuales con el entorno físico real, dando como resultado una realidad mixta. En lugar de reemplazar la realidad física como en el caso de la realidad virtual, se incorpora información virtual mediante una serie de dispositivos a la información física existente. De esta manera, la información se vuelve digital e interactiva.

Funcionamiento de la RA

Para poder utilizarlo es necesario acceder a un dispositivo como una tablet, smartphone, notebook, que debe tener una cámara, una pantalla y un software de Realidad Aumentada con sus respectivos “activadores” (como por ejemplo los códigos QR). Esta otra vía de obtener información nos permite ampliar el acceso al conocimiento y sacar mayor provecho a las herramientas digitales con las que contamos.

Algunas aplicaciones populares de RA son:

• Layar
• Junaio
• Aumentaty

¿Cómo aplicar la Realidad Aumentada en la educación?

En la actualidad, se utilizan aplicaciones de RA en proyectos educativos en exhibiciones, museos o parques temáticos. Pero además está alcanzando mayor protagonismo en las áreas del conocimiento, ya que se ha convertido en una herramienta de gran utilidad en un aula. Algunos ejemplos de aplicaciones en la educación son:

1. Libros de texto: Se puede mejorar su nivel incorporando la posibilidad de visualizar objetos o imágenes en 3D. Aquí puedes ver un ejemplo muy interesante.
2. Geolocalización: La RA puede proveer información sobre la ubicación física o crear escenarios basados en la geolocalización.
3. Educación infantil: Podría aplicarse para que los niños puedan explorar su realidad desde una perspectiva diferente. Un ejemplo es ZooBurst, con el que se pueden crear libros interactivos.
4. Educación online: Puede incorporarse a la educación virtual o e-learning, así como también a juegos virtuales con fines educativos.
5. Educación en general: Se puede integrar a diversas asignaturas como ciencias, matemáticas, idiomas, educación física, etc. En definitiva depende de la imaginación del educador, ya que esta herramienta tiene un gran número de posibles aplicaciones. Puedes encontrar un ejemplo de la aplicación de la RA en un Zoo o un ejemplo de aplicación en la biología en Learnar.

El siguiente video muestra que la manera en la que uno aprende también puede evolucionar.

Fuente: http://blog.tiching.com/realidad-aumentada-la-educacion-del-futuro-ya-esta-presente/